What:什么是模型量化
简单来说,模型量化(Model Quantization)就是通过某种方法将浮点模型转为定点模型。比如说原来的模型里面的权重(weight)都是float32,通过模型量化,将模型变成权重(weight)都是int8的定点模型。
Why:为什么需要模型量化
随着深度学习(Deep Learning)的发现,其在计算机视觉(Computer Vision, CV)和自然语言处理(Natural Language Processing,NLP)等领域都取得了巨大的成功。通过深度学习,我们可以得到用于处理各种任务的高性能模型,这些模型大多都很复杂、一般只适合在GPU上进行推理,并不适合在板端进行推理,然而在实际应用时,很多场景都需要将模型部署到板端。
为了解决模型难以部署到板端的问题,我们就需要通过模型量化来降低模型的复杂性,这个过程不可避免的会发生精度损失。
量化前的浮点模型和量化后的定点模型的特点:
| 量化前的浮点模型 |
量化后的定点模型 |
| 参数量大(float32) |
压缩参数(int8) |
| 计算量大 |
提升速度 |
| 内存占用多 |
内存占用少 |
| 精度高 |
精度损失 |
How:怎么进行模型量化
模型量化就是建立一种浮点数据和定点数据间的映射关系,使得以较小的精度损失代价获得了较大的收益,要弄懂模型量化的原理就是要弄懂这种数据映射关系。
线性量化与非线性量化
线性量化
采用相同的量化间隔对输入作量化
根据Z (zero_point) 是否为0,线性量化可以分为对称量化和非对称量化
非对称量化
浮点0对应的值不是定点0
浮点和定点之间的映射公式:
Q = clamp(Round(R/S + Z)) = Qmax, R∈float且R>Tmax
Q = clamp(Round(R/S + Z)) = Round(R/S + Z), R∈float且Tmin<R<Tmax
Q = clamp(Round(R/S + Z)) = Qmin, R∈float且R<Tmin
R = (Q - Z) * S
其中,Q表示量化后的定点数,R表示量化前的浮点数,Z就是zero_point,即浮点数映射到定点之后,浮点0所对应的定点值。S就是scale,即缩放尺度。Round()函数就是四舍五入。clamp()函数的作用是把一个值限制在一个上限和下限之间。Tmax表示浮点数的最大阈值,Tmin表示浮点数的最小阈值。Qmax表示定数的最大值,Qmin表示定点数的最小值。
通过换算可以得到阈值和线性映射参数 S 和 Z 的数学关系,在确定了阈值后,也就确定了线性映射的参数。
S = (Tmax - Tmin) / (Qmax - Qmin)
Z = Qmax - Tmax/S
| 数据类型 |
取值范围 |
| float32 |
-2^31 ~ 2^31-1 |
| int8 |
-2^7 ~ 2^7-1 (-128 ~ 127) |
| uint8 |
0 ~ 2^8-1 (0~255) |
从上述的映射关系中,如果知道了阈值,那么其对应的线性映射参数也就知道了,整个量化过程也就明确了。
那么该如何确定阈值呢?
一般来说,对于权重的量化,由于权重的数据分布是静态的,一般直接找出 MIN 和 MAX 线性映射即可;而对于推理激活值来说,其数据分布是动态的,为了得到激活值的数据分布,往往需要一个所谓校准集的东西来进行抽样分布,有了抽样分布后再通过一些量化算法进行量化阈值的选取(饱和量化)。
举例:
模型训练后权重或激活值往往在一个有限的范围内分布,如权重值范围为[-2.0, 6.0],即Tmax = 6.0,Tmin = -2.0(非饱和量化)。然后我们用int8进行模型量化,则定点量化值范围为[-128, 127],即Qmax = 127,Qmin = -127,那么S和Z的求值过程如下:
S = 6.0 - (-2.0) / (127 - (-128)) = 8.0 / 255 ≈ 0.03137255
Z = 127 - 6.0 / 0.03137255 ≈ 127 - 191.25 ≈ -64.25 ≈ -64
可以得到如下对应关系:
| 浮点数 |
定点数 |
| 6.0 |
-128 |
| 0 |
-64 |
| -2.0 |
127 |
得到量化参数S和Z后,我们就可以求任意一个浮点数对应的定点数,比如说有一个权重等于0.28,即R=0.28
Q = 0.28 / 0.03137255 + (-64) ≈ -55
对称量化(一种特殊的非对称量化)
浮点0对应的值就是定点0。对称量化对于正负数不均匀分布的情况不够友好,比如如果浮点数全部是正数,量化后的数据范围是[0, 127], [-128, 0]的范围就浪费了,减弱了int8数据的表示范围
非线性量化
对输入进行量化时,大的输入采用大的量化间隔,小的输入采用小的量化间隔。
饱和量化与非饱和量化
一般而言,待量化 Op 的权重采用非饱和量化方法,待量化 Op 的激活(输入和输出)采用饱和量化方法
非饱和量化
非饱和量化是最本质也是最暴力的方法,即通过统计网络模型中每一个层中权重或激活值的绝对最大值,将其映射到127,来计算出缩放因子scale,然后使用线性映射的方式将原始的浮点数据转换到INT8的数据域中,如下图(图是从知乎帖子中拿来的,图中-127应该替换为-128)
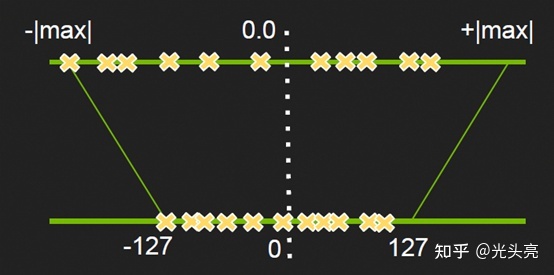
饱和量化
因为模型数据(一般是激活数据)分布可能是不均匀的,直接使用非饱和量化会使得量化后的值都挤在一个很小的范围从而浪费了INT8范围内的其他空间,也就是说没有充分利用INT8(-128 ~ 127)的值域。因此我们在量化时,不是直接将数据的最大值映射到127,而是使用 KL 散度计算一个合适的阈值,将其映射为127。这样使得映射后的-128 ~ 127范围内分布相对均匀,也相当于去掉了一些不重要的因素,保留了主要成分。饱和量化如下图所示(图是从知乎帖子中拿来的,图中-127应该替换为-128)。
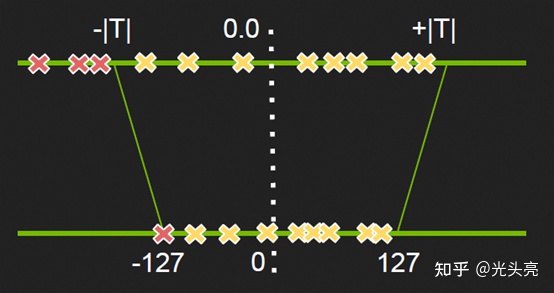
PTQ 与 QAT
后训练量化(Post-Training Quantization, PTQ)
后训练量化(PTQ)可以在没有原始的训练过程的情况下,就能将预训练的FP32模型直接转换为定点模型络。PTQ最大的特点就是不需要数据或者只需要很少的校准数据集。且PTQ几乎不需要调整超参数,使得我们可以很方便的进行模型量化
量化感知训练(Quantization Aware Training, QAT)
模型量化过程其实就是在做一件事,就是找阈值或者scale。
在PTQ中,阈值或者scale一般是通过统计的方法,然后人工通过一些分布相似性得到的,然而,这肯定是有误差的。而且,由于量化是每层独立进行的,所以每层的量化是不依赖于前一层量化的结果的,这就导致了在实际的inference过程中会出现误差累积的情况,进一步影响量化后的性能。所以,我们需要一种可学习的scale。QAT就是在做这样一件事情。
简单概括就是,我们在网络训练过程去模拟量化,我们通过设定一个可学习的scale,这个scale一般可以与权重或者激活值相绑定,然后我们利用一个量化过程 q = round(r/s)*127,将需要量化的值量化到0-127之间,再接着一个反量化过程q * s,就实现了一个误差的传递,接着我们利用反量化后的结果继续前传,最后得到loss,我们求量化后权重的梯度,并用它来更新量化前的权重,使得这种误差被网络抹平,让网络越来越像量化后的权重靠近,最后我们得到了量化后的缩放因子s。而这一系列操作都可以写成网络中的一个op,实现网络的正常训练。
再推荐一篇模型量化的文章:https://zhuanlan.zhihu.com/p/132561405