生活中到处都是那些数据不能以我们期望的方式说服人们的情况。在现实世界中，这种情况相当普遍。任何在节假日晚餐时分与亲戚争论过的人都可能注意到了，通常情况下你给出的相反数据越多，他们似乎就越相信自己的先验信念。
为了充分理解贝叶斯推理，我们需要从数学上理解为什么会出现这样的情况。这将有助于我们在统计分析中识别和避免这些情况。
来源 | 《趣学贝叶斯统计：橡皮鸭、乐高和星球大战中的统计学》作者 | [美] 威尔·库尔特（Will Kurt）译者
| 王凌云
1有超能力的朋友掷骰子
假设一个朋友告诉你，他能以90%的准确率预测掷6面骰子的结果，因为他有超能力。你很难相信这个说法，所以用贝叶斯因子进行假设检验。和“神秘预言家”的例子一样，你需要比较两个假设：
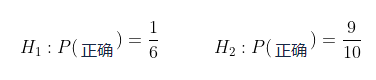
第一个假设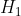 
代表你相信骰子是均匀的，且这位朋友没有超能力。如果骰子是均匀的，我们有 
的机会猜对结果。第二个假设 
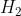代表了朋友的信念，即他真的可以在90%的时间里正确预测掷骰子的结果，因此给出的概率值为 
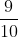。接下来我们需要一些数据来验证他的说法。假设朋友掷骰子10次，正确猜出结果9次。
1 比较似然
先来看贝叶斯因子，现在假定两个假设的先验胜率相等。似然比则可以用下式表示：
所得的结果可以告诉我们，朋友声称自己有超能力的说法在解释数据方面要比你的假设好多少（或差多少）。在这个例子中，为简洁起见，我们将使用变量BF来表示“贝叶斯因子”。由于朋友在10次中预测对了9次，因此我们可以得到如下的计算结果：
所得的似然比表明，朋友有超能力的这个假设解释数据的能力是他只是很幸运的这个假设的468
517倍。这有点令人担忧。根据贝叶斯因子评估准则，这意味着我们应该十分确定 是真的，即朋友拥有超能力。除非你已经对超能力的可能性深信不疑，否则总感觉这里有问题。
2 结合先验胜率
那些仅凭似然就给出奇怪结果的情况中，结合先验胜率大多就可以解决问题。显然，我们相信朋友假设的程度远不如相信自己假设的程度，所以用强大的先验胜率来支持你的假设是有意义的。一开始就可以把先验胜率设置得足够小，这样就可以抵消贝叶斯因子的作用，然后看看能否解决问题：
计算出完整的后验胜率后，我们发现，你还是不相信朋友有超能力这一假设：
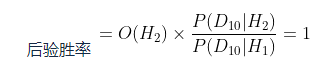
现在，先验胜率再一次将我们从仅考虑贝叶斯因子时会出现奇怪结果的问题中拯救了出来。
假定朋友继续掷骰子5次，并成功预测出5次的结果。现在我们就有了一组新的数据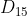 
，它代表掷骰子15次，朋友猜对了其中14次的结果。现在计算后验胜率，我们会发现，即使先验胜率很小也于事无补：
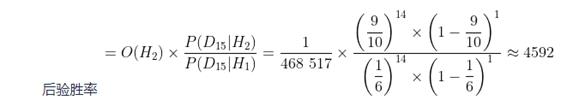
我们使用的还是前面的先验胜率，再加上又猜对5次掷骰子的结果，后验胜率就约等于4592，这意味着我们需要再次肯定朋友有超能力。
在前面的大多数问题中，我们通过添加一个正常的先验胜率来纠正不符合直觉的后验结果。但是现在我们已经添加了一个相当极端的先验来表示反对朋友拥有超能力，后验胜率仍然强烈支持朋友有超能力这一假设。
这是一个很重要的问题，因为贝叶斯推理应该与我们的日常逻辑保持一致。显然，掷15次骰子，猜对其中14次的结果是很不寻常的，但它很难让人们相信猜测者真的拥有超能力。然而，如果不能用假设检验解释这里发生了什么，那就意味着我们不能依靠假设检验解决日常生活中的统计问题。
3 考虑备择假设
这里的问题是，我们不愿意相信朋友有超能力。如果在现实生活中发现这种情况，你很可能会很快得出其他的结论。例如，你可能认为朋友使用的是作弊用的灌铅骰子，在90%的情况下会掷出某个数值。这是第三种假设，而前面的贝叶斯因子只关注了两种可能的假设：骰子是均匀的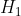（），以及朋友有超能力（）。
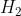到目前为止，贝叶斯因子告诉我们，朋友有超能力的可能性要远远大于他猜对掷均匀骰子的结果的可能性。从当前结果来看，骰子均匀的可能性极小，当我们这样考虑结论时会更有意义。之所以不愿意接受 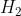这个备择假设，是因为根据对世界的信念，我们并不认为 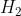是一个合理的解释。
重要的是要明白，假设检验只能比较一个事件的两种解释，但很多时候其实有无数种可能的解释。如果获胜的假设不能说服你，你任何时候都可以考虑第三种假设。
下面来看看，将获胜的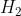假设 与新的假设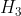 
（骰子被操纵了，因而90%的时间会出现某种固定的结果）进行比较会发生什么。
我们以一个新的关于 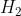的先验胜率开始，并称之为 
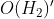（撇号是数学中常见的符号，意思是“类似但不相同”），它表示 
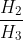的胜率。假如，我们认为朋友使用灌铅骰子的可能性是他拥有超能力的可能性的1000倍（真正的先验胜率可能更极端）。这意味着朋友拥有超能力的先验胜率是 
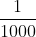。如果重新审视新的后验胜率，我们会得到以下结果，这个结果很有趣：
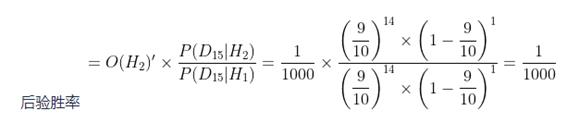
根据上面的计算，后验胜率等于先验胜率 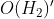。出现这种情况是因为这两种假设的似然相等。换句话说，
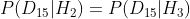。具体到这两种假设，就是朋友正确猜出掷骰子结果的似然与使用灌铅骰子的似然相同，因为我们给这两种假设分配的成功概率本就相等。这也意味着相应的贝叶斯因子始终为1。
这样的结果与我们的日常直觉相当吻合。毕竟，抛开先验胜率不谈，每种假设都能很好地解释我们看到的数据。这意味着，如果在考虑数据之前，我们就认为一种解释的可能性要远远大于另一种，那么再多的新数据也不会改变我们的想法。观察到的数据不再有问题，因为我们找到了更恰当的解释。
在这种情况下，再多的数据也改变不了我们更相信 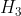而不是 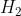，因为两者都能很好地解释所观察到的情况，而且我们已经认定 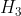是比 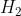更有可能的解释。有趣的是，我们会发现，即使先验信念完全是非理性的，我们也会出现这种状况。也许你非常相信存在超自然现象，也认为你的朋友是地球上最诚实的人。在这种情况下，你可能会把先验胜率定为 
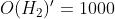。但如果你真的这样认为，那么再多的数据也无法令你相信朋友使用了灌铅骰子。
遇到这样的情况，重要的是要意识到，如果想解决一个问题，你得愿意改变自己的先验信念。如果不愿意放弃不合理的先验信念，那么你必须承认，自己并没有以贝叶斯的方式或逻辑推理。我们都有一些非理性的信念，只要不试图用贝叶斯推理证明它们，那就完全没有问题。
2与亲戚和阴谋论者争论
如果在节假日晚餐时分与亲戚讨论过政治、气候变化或者最喜欢什么电影之类的话题，那么任何人都会有这样的亲身经历：他们在比较的两个假设都能很好地解释数据（对争论的人来说），但只有一开始的先验保留了下来。如果再多的数据都改变不了任何事情，那么怎么改变别人或者自己的信念呢？
我们已经看到，如果比较的是“朋友使用的是灌铅骰子”和“他有超能力”这两个信念，再多的数据也不能让你相信朋友有超能力。这是因为你的假设和朋友的假设都能很好地解释数据。为了让你相信他有超能力，你的朋友必须改变你原来的信念。例如，既然你怀疑他使用的是灌铅骰子，他可以让你选择使用的骰子。如果在你买了一个新的骰子后，你的朋友能继续准确地预测结果，你很可能就开始相信他有超能力的说法了。每当你遇到有两个假设能同等地解释数据的情况时，这一逻辑总是成立。此时，你必须看看在你的先验中有哪些是可以改变的。
假设在你购买了新骰子后，你的朋友依然能够正确地预测结果，但你仍然不相信他有超能力。你现在认为他一定有一种秘密的投掷方式。作为回应，朋友让你替他掷骰子，并且他继续成功地预测所掷点数——但你仍然不相信他。在这样的场景中，除了潜在的假设之外，还有其他的事情发生。现在你又有一个新假设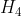 
，即朋友在作弊。你是不会改变自己的想法的。这意味着，对任何 
，都有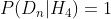 
。显然，这已经超出了贝叶斯统计的范畴，因为你本质上已经承认自己不会改变想法。不过还是要看看，如果朋友坚持要说服你，在数学上会发生什么。
来看看 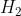和 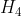这两种解释在使用数据 
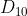（正确预测9次，错误1次）时的比较情况。此时的贝叶斯因子为：
因为你拒绝相信除了朋友在作弊之外的任何事情，所以你观察到的朋友作弊的概率将是而且永远是1。虽然这条数据与朋友有超能力的情况下我们所期望的完全一致，但我们发现自己的信念解释这条数据的程度要好26倍。你的朋友下定决心要改变你顽固的想法，于是他持续掷了100次骰子，正确预测90次，错误10次。这时，贝叶斯因子变得非常奇怪：
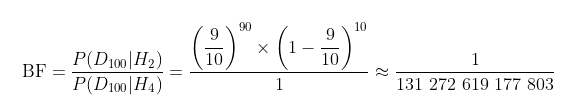
尽管数据强烈地支持朋友的假设，但由于你拒绝改变自己的观点，因此现在你更加坚信自己是对的。当我们完全不允许自己的思想被改变时，更多的数据只会进一步地让我们相信自己是正确的。
那些与政治上激进的亲戚或坚定的阴谋论者辩论过的人，可能非常熟悉这种情景。在贝叶斯推理中，信念至少是可以被证伪的，这一点至关重要。在传统科学中，可证伪意味着某些东西可以被证明是错误的，但在这个案例中，它只表示必须有某种方法来削弱我们对一个假设的信念。
在贝叶斯推理中，不可证伪的危险不在于它们不能被证明是错误的，而在于它们甚至会被那些看起来相矛盾的数据所强化。你的朋友不应该一直坚持说服你，而应该先问：“让你看到什么才能改变你的想法？”如果你的回答是没有什么能够改变你的想法，那么你的朋友最好不要再向你提供更多的数据。
因此，下次与亲戚就政治或阴谋论辩论时，你应该先问他们：“什么数据会改变你的想法？”如果他们没有答案，你最好不要试图用更多的数据佐证自己的观点，因为这样做只会让他们更加坚定自己的信念。
出自：https://mp.weixin.qq.com/s/WM0BSluJxxhWdR7_fzgxhQ