推理能力作为一种可能的“象征着真正的智慧”的能力,在过去的几年里兴许不是被探索和研究得最多的,但肯定是被讨论得最为热烈的。
相关工作分成三个主要的类型,思维链提示 (CoT Prompt) ,一个生成器加一个验证器(生成器负责生成多个推理路径,验证器用于评估这些生成的解答,并选出最终的答案),以及两种的混合方法。
1. 思维链概念的开山之作——Chain-of-Thought Prompting
思维链(Chain-of-Thought,CoT)的主要思想是通过向大语言模型展示一些少量的样例,在样例中解释推理过程,大语言模型在回答提示时也会显示推理过程。这种推理的解释往往会引导出更准确的结果。
以一个数学题为例:

可以看到模型无法做出正确的回答。但如果说,我们给模型一些关于解题的思路,就像我们数学考试,都会把解题过程写出来再最终得出答案,不然无法得分。CoT 做的就是这件事,示例如下:

简单来说,语言模型很难将所有的语义直接转化为一个方程,因为这是一个更加复杂的思考过程,但可以通过中间步骤,来更好地推理问题的每个部分。
CoT 就是把一个多步骤推理问题,分解成很多个中间步骤,分配给更多的计算量,生成更多的 token,再进行求解。
CoT 能解决的问题很多,除了上述的数学应用题,还有常识推理、以及符号推理这类任务,下面补充几个例子方便理解:
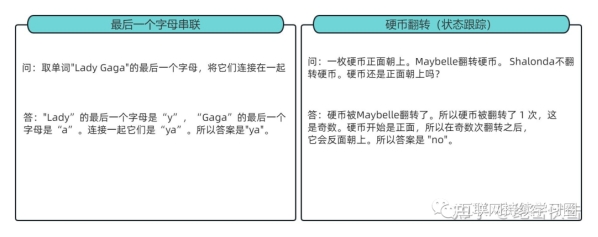
思维链用在数学推理、常识推理、符号推理的例子。绿色是数学推理,黄色是常识推理,蓝色是符号推理:
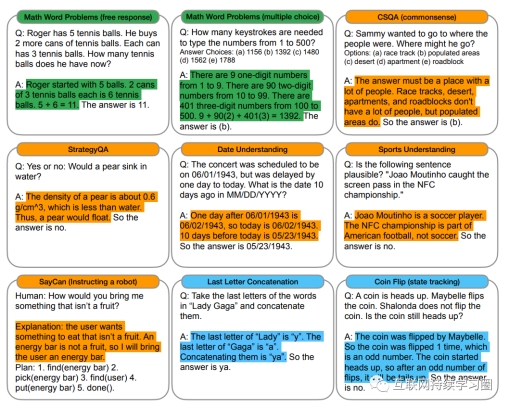
需要注意的是,思维链能力只有在特定大小的模型中才会出现。对于10B以下小模型来说,思维链可能会影响性能。以下是62B模型回答错误,但540B模型回答正确的例子:

2. Zero-shot-CoT
零样本思维链(Zero Shot Chain of Thought,Zero-shot-CoT)提示过程是对 CoT prompting 的后续研究,引入了一种非常简单的零样本提示。他们发现,通过在问题的结尾附加“Let's think step by step”这几个词,大语言模型能够生成一个回答问题的思维链。从这个思维链中,他们能够提取更准确的答案。
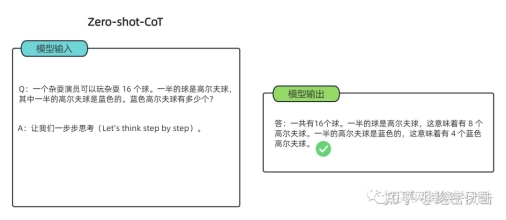
其实 Zero-shot-CoT 是一个 pipeline。也就是说“Let's think step by step”这句话,只是通过这个 prompt 让LLM 尽可能生成一些思考过程,然后再将生成的 rationale(理由) 和 question 拼在一起,重新配合一个answer 指向的 prompt 如“The answer is ”来激励模型生成答案。
从技术上讲,完整的零样本思维链(Zero-shot-CoT)过程涉及两个单独的提示/补全结果。在下图中,左侧生成一个思维链,而右侧接收来自第一个提示(包括第一个提示本身)的输出,并从思维链中提取答案。这个第二个提示是一个自我增强的提示。

作者还做了解释,说明这句“Let's think step by step”是经过验证的,比如对比下面的其它的 instruction,尤其那些不相关的和误导的,效果就非常差,说明大模型真的是在理解这句 instruction 的意思。

3. 多数投票提高CoT性能——自洽性(Self-consistency)
这篇文章是 CoT 后很快的一个跟进工作,是 CoT 系列改进的重要一步。这篇文章几乎用的和 CoT 完全一样的数据集和设置,主要改进是对答案进行了多数投票(majority vote),并且发现其可以显著地提高思维链方法的性能。
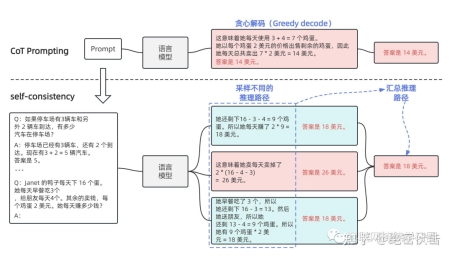
文章提出的方法叫自洽性(Self-consistency),是对 CoT 的一个补充,它不是生成一个思路链,而是生成多个思路链,然后取多数答案作为最终答案。
在下面的图中,左侧的提示是使用少样本思维链范例编写的。使用这个提示,独立生成多个思维链,从每个思维链中提取答案,通过“边缘化推理路径”来计算最终答案。实际上,这意味着取多数答案。
4. Tree-of-Thoughts思维树(ToT)
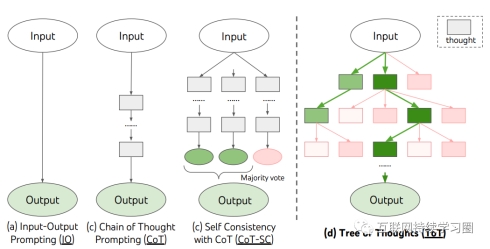
与在链中推理的CoT不同,ToT以树的形式组织其解决问题的策略。每个节点都被称为“思维”,是一个连贯的语言序列,是通往最终答案的一步。

ToT的优势在于其有条不紊的组织。首先,系统会将一个问题分解,并生成一个潜在推理步骤或“思维”候选者的列表。然后,对这些想法进行评估,系统会衡量每个想法产生所需解决方案的可能性。最后,研究者将这种基于语言的生成和评估多样思维的能力与搜索算法相结合,例如广度优先搜索(BFS)或深度优先搜索(DFS),这些算法允许对思维树进行系统性的探索,并具备展望和回溯功能。下面对这些步骤进行具体介绍:

1)思维分解。如表 1 所示,根据不同的问题,思维可以是几个单词(填字游戏),一个等式(24 点游戏),或者是一段写作计划(创意写作)。一般来说,思维应该足够小,以便 LM 能生成多样化的样本,但思维又应该足够大,以便 LM 可以评估其解决问题的前景。
2)思维生成器 G (p_θ, s, k)。给定树状态 s = [x, z_1・・・i],该研究利用两种策略来为下一步思维 step 生成 k 个候选对象。
3)状态评估器 V (p_θ, S)。给定不同状态的边界,状态评估器评估它们在解决问题方面的进展,以确定哪些状态应该继续探索,以及以何种顺序进行探索。
4)搜索算法。最后,在 ToT 框架内,可以根据树结构即插即用不同的搜索算法。本文探索了两个相对简单的搜索算法:广度优先搜索(BFS)和深度优先搜索(DFS)。
5. Graph-of-Thoughts思维图谱(GoT)
思维图(GoT)框架是CoT和ToT方法的更进一步。
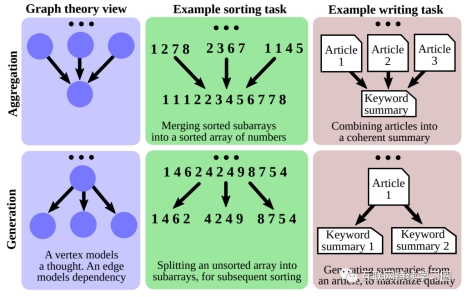
思维图(GoT)的关键是能够将 LLM 生成的信息建模为任意图,其中信息单位是顶点,边代表顶点之间的依赖关系。使用 GoT,通过构建有多于一条输入边的顶点,可以将任意思维聚合起来。整体而言,GoT 使用的图抽象方法可无缝地将 CoT 和 ToT 泛化到更复杂的思维模式,而且这个过程无需更新模型。
图中的有向边描述了这些思想之间的相互依存关系。具体地说,如果一条边从思维t1延伸到t2,则表示t2是基于t1构思的。

具体来说,推理过程被建模为一个有向图 G = (V, E),其中 V 是一组顶点,E ⊆ V × V 是一组边。一个顶点包含对当前问题的一个解答,不管这个问题是最初的问题、还是中间问题或最后的问题。这种思维的具体形式取决于用例;其可能是一段文本(在写作任务中),也可能是一个数值序列(在排序任务中)。有向边 (t_1, t_2) 表示思维 t_2 的构建方式是将 t_1 用作「直接输入」,即通过明确指示 LLM 使用 t_1 来生成 t_2。
GoT的新颖之处在于它能够对这些想法进行转换,进一步完善推理过程。从数学形式上讲,每个这样的变换都可以建模成 T (G, p_θ),其中 G = (V, E) 是反映推理当前状态的图,p_θ 是所使用的 LLM。T 修改 G 的方式通常是通过添加新顶点及其传入边。于是有 G′ = T (G, p_θ) = (V′, E′),其中 V′ = (V ∪ {V^+}) \ {V^−} 且 E′ = (E ∪ {E^+}) \ {E^−}。V^+ 和 E^+ 是注入到 G 中的新顶点和边,它们分别建模的是新的思维和它们的依赖关系。为了最大化 GoT 的表达能力,用户还可以删除思维,做法是指定要删除的相应顶点和边(分别为 V^− 和 E^−)。
主要的转变包括:
聚合变换:即将几个想法融合成一个统一的想法。用户可以使用 GoT 将任意思维聚合成新思维,实现取长补短。使用图模型,可以轻松实现聚合变换:通过添加来自建模了几条链中最后思维的顶点 v_1, ..., v_k 的传出边,使之指向组合这些链的单个思维 v^+,即V^+ = {v^+} 且 E^+ = {(v_1, v^+), ...,(v_k, v^+)},其中 v_1, ..., v_k 是被融合的 k 个思维。更一般而言,这能实现对推理路径的聚合,即更长的思维链,而不只是单个思维。
细化变换:对单个思想进行连续迭代,以对其进行细化:V^+ = {} 和 E^+ = {(v, v)}。这个循环表示与原始思维有同样连接的迭代版思维。
生成变换:有利于从现有思想中产生新的思想,即用户可以基于已有的单个思维 v 生成一个或多个新思维。这一类别中包含 ToT 或 CoT-SC 等更早期方案中的类似推理步骤。从数学形式上讲,有:V^+={v_1^+, …, v_k^+},E^+={(v, v_1^+), …, (v, v_k^+)}。

上图中详细的模块介绍如下:
「提示器」:为 LLM 准备消息或提示。提示应包含图形结构的编码。
「解析器」:从LLM输出中提取相关信息,从而形成存储在每个想法中的状态。
「评分」:验证思想状态是否满足正确性条件并为其分配分数(来自LLMs或人类注释者)。
「控制器」:协调推理过程并决定如何进行。值得注意的是,控制器选择应应用于底层图的思维转换,将此信息传达给提示器,并根据评分器对生成的思维状态的输出来决定推理过程是否已完成或应继续前进。在整个过程中,控制器维护两条信息:
「操作图」:用户定义的静态结构,在推理过程之前创建,并捕获思维操作的执行计划。
「图推理状态」:跟踪LLM推理过程状态的动态结构,包括所有想法及其状态。
6. Program of Thoughts思维程序(PoT)
思维程序(PoT)是一种独特的LLM推理方法。它不仅仅生成自然语言答案,而是要求创建一个可执行程序,可以在Python等程序解释器上运行,从而产生实际的结果。
这种方法强调将推理分解为顺序步骤,并将语义与变量相关联。因此,PoT提供了一个更清晰、更具表达力和基础的答案推导模型,提高了准确性和理解力,尤其是对于需要进行数值计算的数学类型逻辑问题。

PoT与公式有两个方面的区别:(1)PoT将公式转化为多步骤的“思考”过程,(2)PoT将语义与变量绑定,帮助模型以语言为基础进行生成。
7. Auto-CoT自动思维链
Auto-CoT提出自动构建带有问题和推理链的演示,其由两个部分组成:问题聚类将给定问题划分成几个聚类,示范抽样从每个聚类中选择一个有代表性的问题,Zero-Shot-CoT和简单的启发式方法生成其推理链。

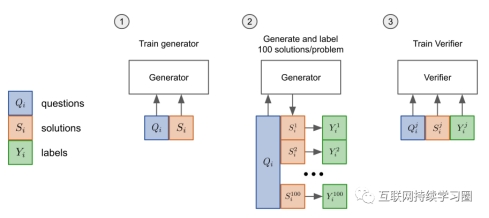
8. Verifiers验证器
本文在生成器的基础上引入一个验证器,使用验证的方式对模型进行训练。具体来说,验证的训练方式包含两个部分:(1) 首先通过微调过程对生成器进行训练;(2)训练得到的生成器用于对问题生成多个高温表达式,这些表达式根据最终得到的结果是否和正确答案相匹配来进行标注,然后用这些表达式和标签去训练验证器。最终得到的验证器用于在测试时对生成器生成的表达式进行打分,分数最高的表达式被用于计算最终答案。实验表明,相比起之前使用单一的生成器进行微调并根据采样概率来选择表达式的方式,引入额外的验证器来选择表达式具有更高的效率。
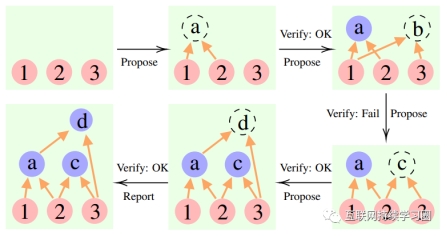
9. Cumulative Reasoning累积推理
同样是将大模型的整体思维过程建模为有向无环图。将所有历史上正确的推理结果存储于内存中,以便在当前搜索分支中探索。
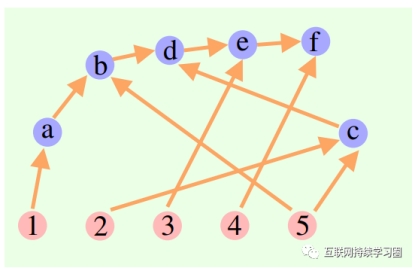
具体来说,这个方法用到了 3 个大语言模型:
·
提议者(Proposer):不断提出新命题,即基于当前思维上下文,建议下一步是什么。
·
·
验证者(Verifier):核查提议者的命题准确性,如果正确就将它添加到思维上下文中。
·
·
报告者(Reporter):判断是否已经能得到最终解决方案,来确定是否结束推理过程。
·
推理过程中,“提议者”先给出提案,“验证者”负责评估,“报告者”决定是否要敲定答案、终止思考过程。
出自:https://mp.weixin.qq.com/s/jOdFKU147x8yRJIL_yMMqg