什么是嵌入?
嵌入是将某些数据对象表示为向量,构造为将数据对象的某些属性编码为其矢量表示的几何属性。
这非常抽象,但并不像听起来那么复杂。
首先,我们需要介绍一点(非常少)数学。向量是两个听起来不同但实际上相同的东西:
1.
向量是多维空间中的一个点。
2.
3.
向量是标量值的有序列表,即数字。
4.
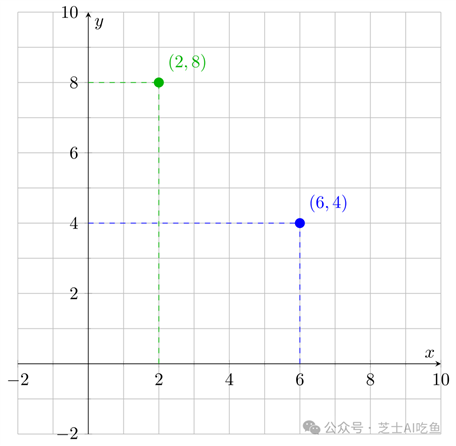
要了解这是如何工作的,请考虑两个数字的列表。例如,$(6,4)$和$(2,8)$。您可以看到我们可以将它们视为x-y轴上的坐标,每个列表对应于二维空间中的一个点:
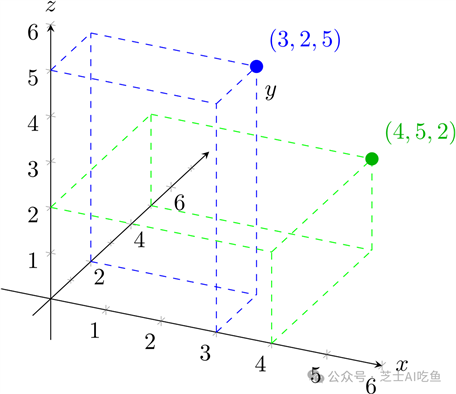
如果我们有三个数字,比如$(3,2,5)$和$(4,5,2)$,那么这对应于三维空间中的点:
重要的是,我们可以把它扩展到更多的维度:4,5,100,1000,甚至数百万或数十亿。绘制一个有一千个维度的空间是非常困难的,想象一个维度几乎是不可能的,但是从数学上讲,这真的很容易。
例如,点$(6,4)$和$(2,8)$之间的距离只是毕达哥拉斯定理的应用。给定两点$a=(x_1,y_1)$和$b=(x_2,y_2)$,它们之间的距离是:
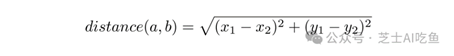
对于$(6,4)$和$(2,8)$,这意味着:
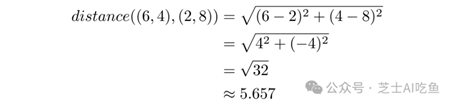
对于三维,我们只需通过添加一项来扩展公式。对于$a=(3,2,5)$和$b=(4,5,2)$:
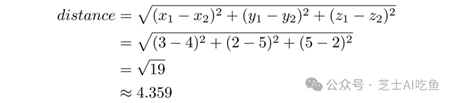
我们可以将这个公式扩展到任意维数的向量。我们只是添加更多的术语,就像我们从二维到三维一样。
除了距离,我们在高维向量空间中使用的另一个度量是两个向量之间夹角的余弦。如果您不仅将每个向量视为一个点,还将其视为距离原点的一条线(由向量$(0,0,0,…)$指定的点),那么您可以计算两个向量之间的夹角(下图中为$\θ$)。
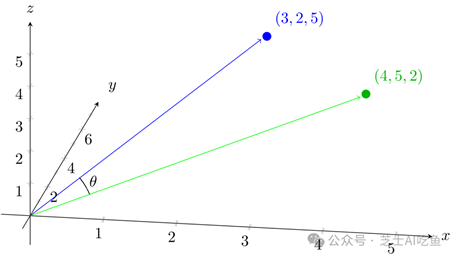
为了计算这个,我们有另一个公式,可以扩展到任意数量的维度。我们知道向量$a$和$b$之间角度$\θ$的余弦是:
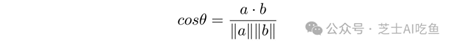
这比看起来要复杂,但不多。$a\cdot b$称为两个向量的点积,很容易计算。如果$a=(3,2,5)$和$b=(4,5,2)$,那么:
至于$||a||$和$||b||$,它们是向量的长度,即从原点到该点的距离。所以:

因此,要计算$cos\theta$:
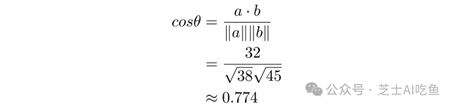
这个余弦对应于大约39.3°的角度,但是在机器学习中,我们通常在计算余弦后停止,因为如果两个向量中的所有数字都大于零,那么余弦的角度将在0和1之间。
这看起来像很多数学,但是如果你仔细看,你会发现它只是加法、减法、乘法、除法、一个指数和一个平方根。简单但无聊和重复的东西。你实际上不必做任何数学运算。我们让电脑在身边的全部原因就是为了做这种事情。但是你应该明白向量是数字列表,理解使用向量的概念,理解如何,不管向量有多少维,我们仍然可以做计算距离和角度之类的事情。
让这一点如此重要的是,我们保存在计算机上的任何数据也只是一个数字列表。如果我们选择这样看待它,每一个数据项——数字图片、文本、录音、3D模型文件,任何你能想到的可以放入计算机文件的东西——都是一个向量。
我们如何为事物分配嵌入向量?
嵌入的目的是为数据对象分配向量,以便它们在高维空间中的位置编码关于它们的有用信息。如果我们选择以这种方式看待数据对象——文本、图像或我们正在处理的任何其他东西——它们已经是向量了。这些向量的位置并没有告诉我们任何关于它们的有用信息。
考虑这四个图像:

每个都是用标准RGB调色板着色的450x450像素图像。这意味着图片由202,500个像素组成,每个像素的红色、绿色和蓝色值在0到255之间有一个数字。将其转换为具有607,500个维度的向量是微不足道的。
我们可以拍摄任何一对图像,计算它们之间的距离或测量它们的余弦,但是苹果之间不太可能特别近或者离橘子特别远。至少,如果我们使用数百张苹果和橘子的照片,而不仅仅是四张,那就不太可能了。
更有可能的是,我们会得到这样的东西:
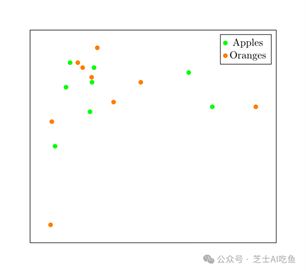
我们无法在60万个维度上画图,所以这张图只用了两个维度来证明这一点:我们应该预期苹果和橘子是半随机放置并混合在一起的。
我们希望为每个图像分配一个独特的嵌入,使得苹果靠近橘子,反之亦然。我们想要这样的东西:
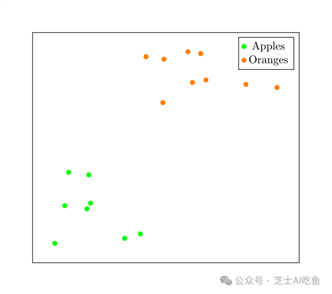
为此,我们构建了一个神经网络(我们称之为嵌入模型),它将607,500个维度向量作为输入,并输出一些其他向量,通常维度较少。例如,广泛使用的ViT-B-32图像嵌入模型将输入图像转换为512维嵌入向量。
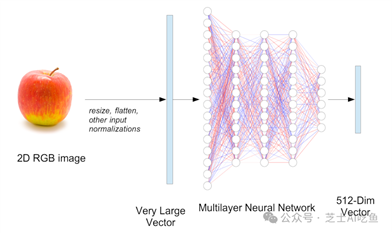
然后我们用苹果和橙子的标注图片训练嵌入模型,指示它慢慢调整网络的权重,以分离苹果和橙子的嵌入向量。经过多次循环训练,我们期望当我们给苹果的模型图片作为输入时,它会输出彼此之间的距离比我们给它橙子图片作为输入时得到的向量更近的向量。
这些输出向量被嵌入,它们共同形成一个嵌入空间。单个嵌入的位置编码了有关其相应数据对象的有用信息:在这种情况下,某物是苹果还是橘子的图片。
区分苹果和橘子是一个非常简单的场景,但是你可以很容易地想象把它标定为许多功能。
在一些用例中,我们甚至可以在没有明确说明哪些特征相关的地方构建嵌入,我们让神经网络在训练过程中弄清楚。例如,我们可以通过拍摄人脸来构建脸部辨识系统,并训练嵌入模型输出嵌入,将同一个人的照片靠近在一起。我们然后可以以他们的嵌入向量为键构建人们图片的数据库。
我们期望存储的面通过嵌入空间分布:

我们可能会期望这个嵌入空间会编码许多我们从未明确训练过的特征。例如,它可能会将男性与女性隔离开来:
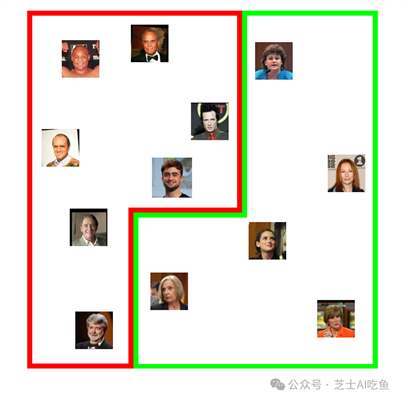
或者我们可能会发现人们根据头发的特征聚集在一起,比如秃顶或灰色:
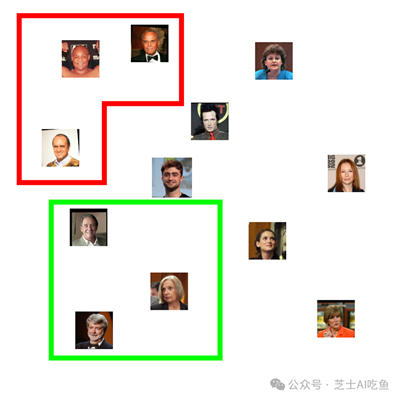
但是我们会期望,如果我们给它数据库中某人的另一张照片,新照片的嵌入将更接近我们存储的那个人的照片,而不是其他任何人:
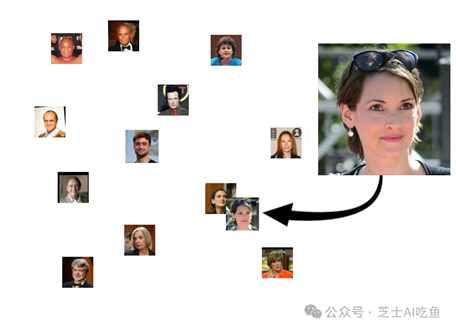
当然,它也会找到看起来相似的人,尽管我们希望他们不会像两个实际上是一样的人那样亲密:
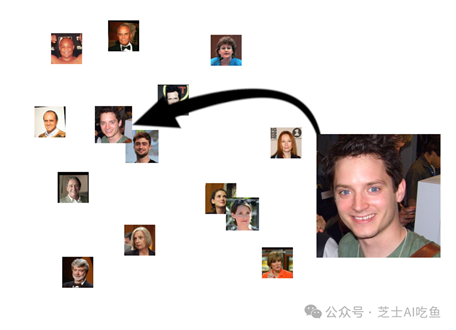
这突出了嵌入空间的逻辑:输入是多种多样的,但是通过将它们转化为嵌入,我们将特征——有时是复杂的、隐藏的、微妙的或不明显的特征——转化为软件可以轻松识别的几何属性。
嵌入空间还可以支持多种输入类型,如文本和图像,创建通用嵌入空间并使您能够在两者之间进行映射。
例如,如果我们有一个带有描述性标题的图片数据库,我们可以共同训练两个嵌入模型——一个用于图像,一个用于文本——在同一个嵌入空间中输出向量。结果是图像描述的嵌入和图像本身的嵌入将彼此靠近。

原则上,任何类型的数字数据都可以作为创建嵌入的输入,任何配对的数据类型——不仅仅是文本和图像——都可以用于创建多模式联合嵌入空间。
嵌入有什么好处?
就像瑞士军刀一样,问题应该是,它们有什么不好?
我们已经展示了如何将嵌入用于图像分类和脸部辨识系统,但这还远远没有用尽可能性。例如,从文本描述(又名“人工智能艺术”)中生成人工智能图像首先为文本和图像构建一个联合嵌入空间,然后,当用户输入文本时,它会计算文本的嵌入,并尝试构建一个将产生附近嵌入的图像。
嵌入是如此普遍有用,以至于它们可以在人工智能和机器学习中看到应用程序。任何需要相似性/不相似性评估、依赖隐藏或不明显特征或需要不同输入和输出之间隐式上下文相关映射的应用程序,都可能以某种形式使用嵌入。
嵌入是现代机器学习和人工智能的一项重要技术,以某种形式出现在人工智能应用程序的范围内。正确理解和掌握这项技术使您能够利用人工智能模型为您的业务增加最大价值。
嵌入背后的理论甚至并不复杂:它只涉及从数据对象到高维向量空间中具有共同属性的点的映射,这些属性对你很重要。使用它们只是测量向量距离和余弦的问题,这是计算上微不足道的数学!
不幸的是,构建和训练嵌入模型的实践比使用它们更复杂。
英文原文链接https://jina.ai/news/embeddings-the-swiss-army-knife-of-ai/
出自:https://mp.weixin.qq.com/s/DGeey6v3ntGhIorOd_eB3w