最近看了Ilya关于泛化的演讲有所感悟,所以总结了这篇文章,作为入门者只是尽力去联系和理解所观察到的现象,不会探讨过于深入的东西,但希望能引起大家的兴趣。
如果你认同Scaling Law定律,你就应该相信通过大量不同的数据来追求长期的模型泛化能力比短期的通过巧妙的模型微调更重要,这个想法在机器学习先驱 Rich Sutton 《苦涩的教训》中也有所体现。
那么什么是泛化能力呢?在《论语》中曾有言,孔子问子贡说,你与颜回比如何?子贡回说,“我无法望其项背,颜回可以举一反十,而我顶多闻一知二”。这种举一反十的能力就是我们常说的泛化能力,可见在孔子看来一个人的泛化能力才是决定了其上限的根本。
在人工智能领域,通俗地说,泛化是指模型在训练数据中学习到的共性,这样在面对从未见过的数据时就能够具备很好的预测能力。
那么怎样以最简单方式提高模型泛化能力呢?为了下文行文方便,这里会将本篇文章想要表达的核心思想做一下定义。
定义1: 模型的泛化程度与你将不同数据推入足够高容量模型的速度成正比。
这个定义可以类比我们教育孩子提升他们的泛化能力的方式。首要的方法是帮助孩子建立坚实的认知基础。
例如,如果孩子从出生开始只见到红色的苹果,那么他们可能会认为只有红色的水果才是苹果。然而,如果我们向他们展示其他颜色的苹果,他们会逐渐意识到苹果的颜色可以多样化。
同样地,对于模型来说,如果我们训练它在大量的多样化数据上进行学习,它就能够更好地适应新的、未曾见过的数据。但有一点需要注意的是,这就需要模型能够吸收这些数据。
所以说,记忆是通向泛化的第一步。
1. 监督学习是优秀的数据海绵
经过监督学习训练的深度神经网络是优秀的数据海绵——它们可以记住大量数据,并且可以通过数万批量大小的训练来快速完成这一任务。
这是因为监督学习最大的优点是具有数学保证,只要你有足够多的数据,并在数据上实现低误差,那么它对新数据的预测也会低误差。换句话说,只有你找到了一个函数降低了在训练集上的误差,那么“学习”就必然会取得成功。当训练模型到达最小化训练损失时,我们可以说它已经“记住”了训练集。
有人可能会说,我们只是在拟合训练集么,为什么能推导出测试集泛化呢?
是的,如果我们已经将数据集中的每一个token都看过了一遍,那么所谓的 "training loss" 其实就是 "next
token validation loss"。
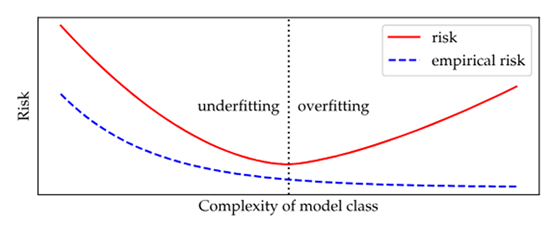
然而,传统的泛化观点认为,随着模型复杂性的增加,最初的经验风险和泛化风险都会降低。然而,过了某个点,泛化风险又开始增加,而经验风险却下降。
如上图所示,许多教科书中显示的图形都是U形风险曲线。低于曲线最小值的复杂度范围称为欠拟合,超过最小值范围称为过拟合。
定义2:狭义上,过度参数化的深度网络可以更好的泛化。
虽然传统上,人们会认为当训练损失最小化到零很快就会出现过度拟合,但过度参数化的深度网络似乎即使在这种情况下也能很好地泛化。
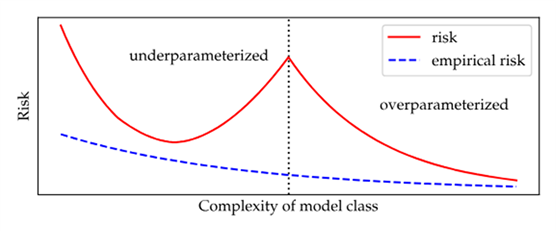
过度参数化的模型,即使在训练损失完全最小化的时候,也可以继续减少风险。在过度参数化的情况下,模型复杂性的增加会继续无限期地降低风险,尽管边际收益会降低,但会趋向于某个收敛点,过度参数化和风险之间的这种经验关系似乎很稳健。
不过上图中的双下降曲线并不具有普遍性,在许多情况下,实际上我们在整个复杂性范围内观察到单一的下降曲线,如下图所示。
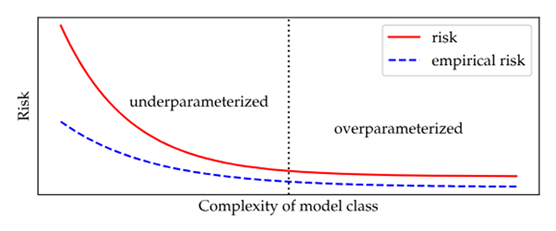
事实上,经验证据表明,较大的模型不仅具有泛化性,而且比较小的模型能够产生更好的样本外预测的特性。这种模型变大所带来的泛化性是否只是把问题推迟了,我们不得而知。
所以从理想的情况下来看,我们有多少标签数据,那么监督学习模型就能够吸收多少数据,所以我们说监督学习是优秀的数据海绵。
当然同时还有一点十分关键:就是测试分布和训练分布必须保持一致,只有在这种情况下,监督学习理论才能发挥作用。
2. 无监督学习是针对不同任务的监督学习
监督学习其特点在于训练数据集中包含带有标签的样本,模型通过这些标签指导以优化特定的目标函数。这意味着模型接收到输入数据后,会根据与之相关联的标签进行学习,并试图建立输入和输出之间的关系。
相反,无监督学习其训练数据集中并不包含标签信息。在无监督学习中,模型被要求自行发现数据中的潜在结构、模式或规律,并进行合适的学习和推断。这种方法的好处在于它可以帮助我们对数据进行探索和理解,找到其中的隐藏特征和关联性,而无需预先知道具体的优化目标。
但无监督学习的问题也非常明显,有时我们优化的是一个目标函数,但我们真正期望模型学到的是另一个目标。
这就引出了一个重要问题:如何确保模型所学到的对我们的目标是有效的呢?特别是在处理无标签数据时,如何确保优化的目标能够在实践中有效应用呢?
Ilya Sutskever 提出可以通过学习数据中的数学结构,即通过分布匹配来实现这一目标。这意味着我们可以让模型学习数据的分布特征,而不仅仅是优化特定的目标函数。通过这种方式,模型可以更好地捕捉数据的本质特征,从而提高泛化能力和对新数据的适应性。
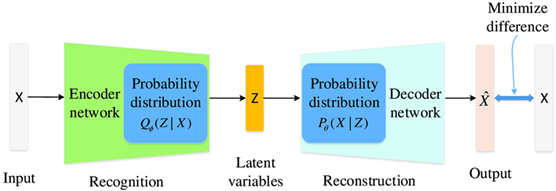
定义3:无监督学习没有样本粒度的标注,因而无法像监督学习那样学习明确的映射f(x)~y;但无监督学习可以在分布之间建立映射作为学习目标,即distribution(F(X))~distribution(Y)。
那么什么是分布匹配?"分布匹配"是指通过找到一个函数 f,使得对于输入数据源 X 生成的分布类似于数据源 Y 的分布。这种方法通常在处理不同语言之间的翻译、文本到语音的转换等领域有着重要的应用。
举个例子,假设我们有一个英语句子的分布作为输入,通过应用函数
f,可以得到与法语句子十分相似的分布。这就意味着找到了函数 f 的真实约束,而且如果 X 和 Y 的维度足够高,那么函数 f
可能会存在大量约束。实际上,几乎能够通过这些信息完整还原出函数 f 的信息。这种方法类似于监督学习,可以保证学习的有效性。

然而,在真实的机器学习环境和无监督学习场景中,上述翻译场景设置可能带有一些人为因素,并不完全符合真实情况。但我们可以做一个思想实验:假设你有两个数据集 X 和 Y,分别对应硬盘上的两个文件,并且拥有一个非常出色的压缩算法 C 来压缩数据。那么,当将 X 和 Y
联合压缩,将它们连接在一起,然后输入到压缩器中时,会发生什么呢?
在这种情况下,一个足够出色的压缩器会利用存在于 X 内部的模式来帮助它压缩 Y,反之亦然。因为要压缩到最小体积,就需要找到其中的共性。
而当我们利用从数据集 X 学习到的压缩模式去压缩另一个数据集 Y 时,就建立了一种分布匹配的映射。这种过程展示了通过理解数据内在的结构和共性,能够实现对数据分布的匹配和学习,它类似于压缩的过程,通过找到数据之间的共性和模式,实现数据分布的匹配和转换。
定义4:压缩就是泛化。对于一个数据集最好的无损压缩,就是对于数据集之外的数据最佳泛化。
压缩的定义可以被理解为找出数据中的规律性、共性,并用更简洁的方式表示数据,以减少冗余信息。而当我们成功地对数据进行压缩时,意味着我们已经捕捉到了数据的本质特征和规律,这和泛化找到数据中的共性是类似的,所以我们可以说“压缩”就是对泛化的一种理解。
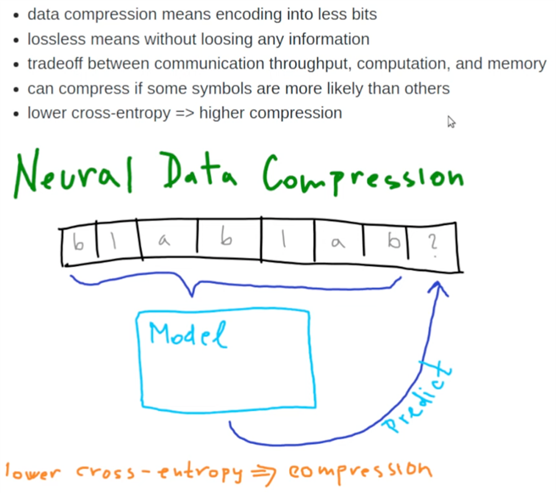
如果我们针对某个数据集实现了最佳的无损压缩时,也就意味着我们尽可能的提炼数据的关键特征。因此,一个能够对数据集进行最佳无损压缩的模型,通常也能够在其他数据集上实现最佳的泛化效果。
计算机教授Marcus Hutter在2006年发起了一个竞赛,名叫Hutter Prize。该竞赛的目标是设计出一个可以在给定数据集上实现最佳压缩率的通用算法。
他在Hutter Prize的官网上说,为了压缩数据,必须找到其中的规律,这本质上是困难的,…能够很好地压缩与智能密切相关。网站的地址:http://prize.hutter1.net/
如果Hutter是对的,那我们就可以通过压缩效率来近似量化模型的智能。
定义5:压缩和预测下一个单词本质上是等价的。
就像Hutter所说的一样,能够实现高效压缩的算法往往能够揭示数据的深层规律,这也是智能的一个重要表现。

对未见数据的下一个token预测的能力就是模型的泛化能力,而优秀泛化的前提就是需要对数据的内在数学规律有深刻理解,即实现对数据的“无损压缩”。
IIya也多次提到“大模型是对世界信息的压缩”的观点,对下一个token的预测让大模型学到了世界的一个压缩表示。
如果将下一个token预测当作压缩模式,那么GPT的升级可能并不需要基于原始数据进行训练,而是基于大模型这个压缩器在分布之间泛化。
3. 涌现是模型对数据的数学结构深层理解和压缩
涌现能力指的是从简单规则中产生复杂行为或高级功能的能力,也称为顿悟。
事实上,一篇ICLR 研讨会论文 Grokking 研究了这种现象,表明如果你在这种零训练损失状态下训练足够长的时间,模型可能会突然顿悟并在很久以后进行泛化(作者称之为“涌现”)。
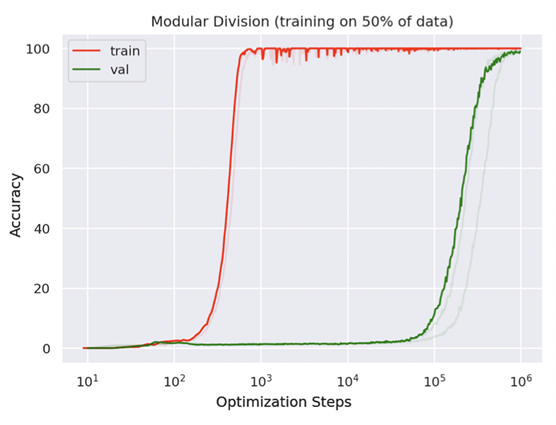
这里有趣的发现是,如上图所示,训练集上很快准确率到达 1,验证集上 "overfitting" 而一直学不会,直到 3 个量级以上的训练步数后,也慢慢会了,准确率趋近于 1。
作者是在一个a + b mod 67的一个小模型上进行实验验证的。首先随机划分所有a,b 配对成测试和训练数据集。经过数千个训练步骤,训练数据用于调整模型以输出正确答案,而测试数据仅用于检查模型是否学会了通用解决方案。
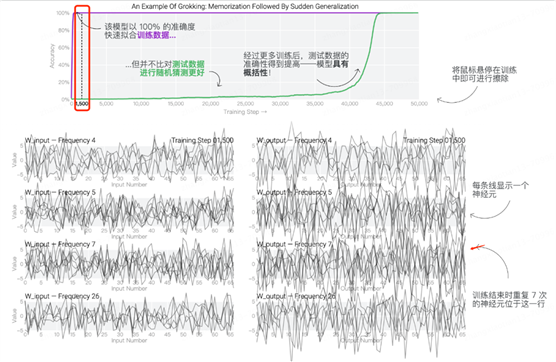
在训练的初始阶段模型的权重是非常嘈杂,当测试数据的准确率已经达到100时,权重的波动依然比较混乱,如下图所示,研究人员根据神经元在训练时的循环频率将其分组,并将每个神经元分别绘制成一条单独的线,可以看出在训练集准确率为1时,波动依然非常混乱。
但随着在测试数据上发生“顿悟”,测试的准确性增加和模型出现泛化,神经元的波动也开始表现出周期性模式,如下图所示:
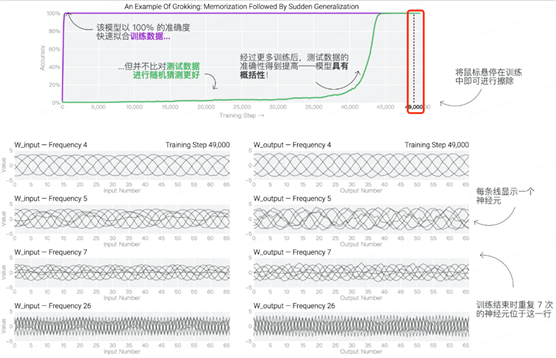
神经元的周期性波动似乎表明其已经从数据中学到了某种数学结构,它所带来的效果也是意想不到的好。
所以我们跳出来看,如果我们可以通过将不同数据推入模型追求长期的模型泛化能力比短期的通过巧妙的模型微调更重要这一原则,扩展到其他无法通过分析算法改进的具有挑战性的问题,会怎么样?
总结
我们希望在训练集上经验风险最小化的模型能够良好地泛化到测试集未见过的数据中,即使两者之间存在一定差距。VC维度、Rademacher复杂度就是衡量和理解模型泛化能力的重要工具。
如果没有过拟合,那么联合压缩就是最大似然估计。如果有一个数据集,那么给定参数的似然之和就是对数据集进行压缩的成本,此外,你还需支付压缩参数的成本。但如果你现在想要压缩两个数据集,那么只需在总和中添加更多的数据集。
当然本文的观点是狭窄的,它限于我们对泛化的理解的不仅仅是缺乏定量的清晰度,或者无法解释重要的经验观察结果,不过Ilya的观点确实也给我们带来更多的启发,希望可以对您有多帮助。
出自:https://mp.weixin.qq.com/s/2d8YoPHFyYMPdu9WKeI4Hg