一 本文概要
本论文探讨了在系统性投资策略开发中,如何通过改进回测技术来避免常见的陷阱和偏差,进而提高策略在样本外的表现。作者分析了三种主要的回测方法,详述了各自的优势和挑战。通过提供关于如何增强模拟质量的指导,以及介绍在多重试验下如何正确计算夏普比率的方法,论文旨在为实践者提供更准确和可靠的投资策略开发工具。
二 背景知识
1. 回测的重要性与常见陷阱1. 回测的重要性与常见陷阱
回测是模拟系统性投资策略在历史数据上的表现,以评估其未来预期风险和收益的关键技术。然而,回测常常因为方法上的缺陷和常见的偏差而被误用。这些问题可能导致过度拟合,使得策略在样本外的表现不佳。常见的陷阱包括生存偏差、前视偏差、数据挖掘偏差等。
2. 多重检验下的选择偏差(SBuMT)2. 多重检验下的选择偏差
在进行多次试验后,只报告最佳结果的做法会引入选择偏差,特别是在多重检验的情况下。这种偏差会导致研究者高估策略的统计显著性,从而增加过度拟合的风险。理解并校正多重检验下的选择偏差,对于确保发现的策略在样本外的有效性至关重要。
3. 夏普比率及其局限性3. 夏普比率及其局限性
夏普比率是衡量投资策略绩效的常用指标,定义为超额收益与收益标准差的比值。然而,夏普比率在收益分布非正态的情况下可能不准确,特别是当策略的收益具有高偏度和峰度时。此外,在多次试验后,夏普比率可能会被高估,因此需要对其进行校正,如使用修正后的夏普比率或引入最小轨迹记录长度等方法。
三 本文方法
作者首先详细介绍了三种主要的回测方法:
1. 滚动前推测试(Walk-Forward Testing) 滚动前推测试(Walk-
滚动前推测试是最广泛使用的回测方法,策略在过去一段时间的历史数据上进行评估。其优点是结果易于分析和解释,但缺点是只测试了单一路径,增加了过度拟合的风险,并假设过去的事件和过程会在未来重复。
2. 重抽样方法(Resampling Method)
重抽样方法包括交叉验证和自助法等技术,通过对过去的观察值进行重抽样,构建新的路径,克服了滚动前推方法只测试单一路径的缺陷。优点是可以评估策略的稳健性,减少过度拟合的可能性,但仍可能不能准确代表未来的表现,且需要适当的数据格式。
3. 蒙特卡洛模拟(Monte Carlo Simulations)
蒙特卡洛模拟要求对数据生成过程有深入理解,能够根据理论构建或统计分析来模拟未来的路径。其优势在于,如果数据生成过程是正确且未改变,所观察到的性能确实可以代表未来的结果。该方法还可以通过监控实时数据的统计特性,检测结构性变化。然而,构建准确的数据生成过程可能非常复杂,尤其是对于异常事件的模拟。
作者进一步讨论了如何提高历史模拟的质量,重点关注以下六个方面:
1.
数据质量
• 生存偏差:仅分析存活的数据而忽略失败的样本,会导致结果偏差。
• 时点数据和数据重述:确保使用在当时可获得的数据,避免因数据重复导致的前视偏差。
• 错误和缺失数据:数据清洗是必要的,包括纠正错误和处理缺失值。
2.
数据代表性
• 样本期选择偏差:选择的时间段可能影响结果,应包括各种市场条件的数据,以确保策略的稳健性。
3.
统计完整性
• 数据挖掘和数据窥视:过度搜索数据可能导致虚假的模式,应避免过度拟合。
• 多重检验下的选择偏差校正:在多次试验后,需要调整统计显著性水平,避免高估结果的显著性。
4.
建模与泛化
• 前视偏差:使用未来数据来做出投资决策,会导致高估策略绩效。
• 引入禁运期:设置一个持出样本的数据集,用于最终验证策略的有效性。
5.
成本和约束
• 交易成本:忽略交易成本会高估策略收益,应考虑佣金、滑点、市场冲击等。
• 卖空限制:卖空成本和限制会影响策略,应在回测中予以考虑。
• 流动性约束:交易量大的策略可能影响市场价格,需要限制交易量。
6.
绩效评估
• 因果关系图:在回测前建立因果关系图,明确策略背后的因果机制。
• 绩效指标:除了夏普比率外,还应考虑最大回撤、风险价值等指标。
• 整体评估:应综合多个绩效指标进行分析,避免片面结论。
• 同行评审:通过独立的同行评审,可以进一步验证策略的有效性。
作者还深入探讨了多重检验下选择偏差的影响,并通过数值示例展示了在多次试验后,如何正确调整统计测试,避免高估策略的显著性。
四 实验分析
作者通过数值模拟,展示了多重试验对统计测试和策略绩效的影响。在每次模拟中,生成10个时间序列,每个序列代表五年的日收益率,均从均值为零的正态分布中抽取。计算每个策略的夏普比率,选择最佳的一个。结果显示,随着试验次数的增加,即使在期望收益为零的情况下,最高的夏普比率也会被高估。
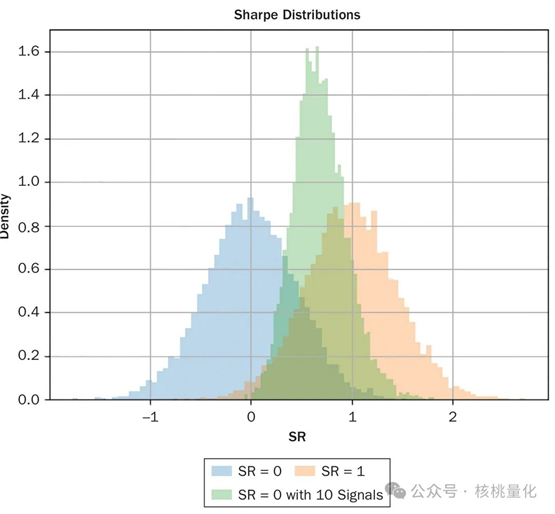
图1展示了在不同场景下夏普比率的分布,包括:
1. 期望夏普比率为0的单次试验(蓝色)
2. 期望夏普比率为1的单次试验(琥珀色)
3. 期望夏普比率为0的10次试验中的最大值(绿色)
结果表明,在多次试验后,最高的夏普比率会偏离正态分布,且传统的单次试验统计测试不再适用。
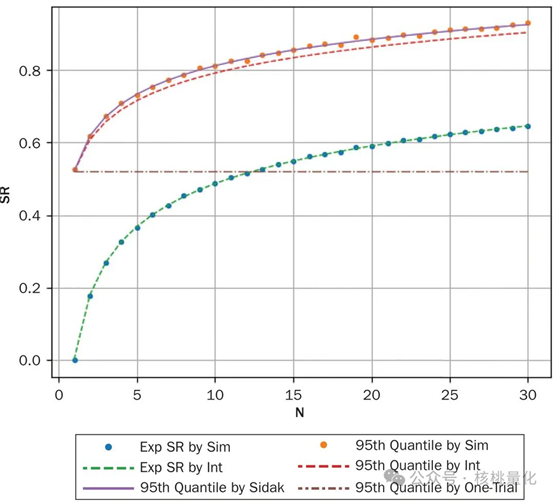
图2显示了随着试验次数的增加,期望的夏普比率和第95百分位的截断值如何变化。可以看出,试验次数的增加会显著提高夏普比率的期望值,强调了在多重检验下进行校正的重要性。
五 总结展望
本论文深入分析了回测在系统性投资策略开发中的关键作用,介绍了三种主要的回测方法,并详细讨论了各自的优势和局限性。通过提出一系列最佳实践,作者为实践者提供了提高回测质量的指导,包括采用因果关系图、使用严格的统计测试、确保高质量的数据以及考虑现实的成本和约束等。
尽管回测是开发投资策略的宝贵工具,但其自身的局限性,如过度拟合和金融市场的非平稳性,意味着实践者应谨慎使用。未来的研究和实践应更多地关注建立在坚实因果理论基础上的策略开发,并在此基础上使用回测进行验证,从而提高策略在样本外的有效性和稳健性。
原文出自:https://mp.weixin.qq.com/s/BBmwErMQWHC1s_304v-9GQ